Empirical Bayes small area prediction

class: center, middle, inverse, title-slide

# Empirical Bayes small area prediction
## under a zero-inflated lognormal model with correlated random effects
### Xiaodan Lyu
### Joint work with Dr.Emily Berg
### 04 February 2020

---

## Basic Setting

- Predictions for small domains are our primary interest.

+ Standard survey estimators are often unreliable given small sample sizes. (Rao, Molina, 2015)

+ Use model to incorporate auxiliary information (known for the whole population).

- Data motivation (CEAP RUSLE2)

+ skewed data with heavy zeros
 
 + potential correlation between the positive part and the binary part

???
area mean, quantiles
around 15% zeros
skewed income data, wine production

---
## Data Model

Suppose response variable `${y}_{ij}^*, i=1,..,D;j=1,..,N_i$` satisfies
`$${y}_{ij}^*=y_{ij}\delta_{ij}$$`
 + Positive part:
`$$\log(y_{ij})=\beta_0+\mathbf{z}'_{1,ij}\boldsymbol{\beta}_1+u_i+e_{ij}$$`
where `$e_{ij} \overset{i.i.d}{\sim} N(0, \sigma^2_e)$`.

+ Binary part: `$\text{Pr}(\delta_{ij}=1) = p_{ij}$`,
`$$g(p_{ij})=\alpha_0+\mathbf{z}_{2,ij}'\boldsymbol\alpha_1+b_i$$`
where `$g(\cdot)$` is the parametric link function to be specified.

---
## Data Model

- Lognormal extension

+ Mathematically tractable and computationally simple.
  
  + SAE lognormal model - Berg and Chandra (2013).

+ SAE zero-inflated lognormal - Lyu (2018).

- Correlated random effects

+ `$$\left(\begin{array}{c} u_{i} \\ b_{i}\end{array}\right) \stackrel{iid}{\sim}  \mbox{BVN}(\boldsymbol{0}, \boldsymbol{\Sigma}_{ub}), \boldsymbol{\Sigma}_{ub} = \begin{pmatrix}\sigma_u^2 & \color{red}{\rho}\sigma_{u}\sigma_{b}\\\color{red}{\rho}\sigma_{u}\sigma_{b} & \sigma_b^2 \end{pmatrix}$$`
  
  + "plug-in" approach of Chandra, Chambers (2016) => implicitly assume independence
  
  + Bayesian approach of Pfeffermann et al (2018) => requires specifying prior distributions
  
???

linear mixed model used for the positive part

---
## Empirical Bayes general

The minimum mean squared error (MMSE) predictor of `$\color{blue}{\zeta_{i} = \frac{1}{N_i}\sum_{j=1}^{N_i}y_{ij}^*}$` is
`$$\hat\zeta_{i}^{\rm{MMSE}}=\frac{1}{N_i}\Big\{\sum_{j \in s_i} y_{ij}^* + \sum_{j \in \bar s_i}\hat{y}_{ij}^{*\rm{MMSE}}\Big\}$$`
where `$\hat{y}_{ij}^{*\rm{MMSE}} = \color{blue}{E_{\theta}(y_{ij}^*|\boldsymbol{y}^*_{s_i})}$`

Let `$\hat{\boldsymbol \theta}$` be a consistent estimator of model parameter `$\boldsymbol \theta$`.
`$$\hat \zeta_{i}^{\rm{EB}}=\frac{1}{N_i}\Big\{\sum_{j \in s_i} y_{ij}^* + \sum_{j \in \bar s_i} \hat y_{ij}^{*\rm{EB}} \Big\}$$`
where `$\hat y_{ij}^{*\rm{EB}}=\hat{y}_{ij}^{*\rm{MMSE}}(\color{red}{\hat{\boldsymbol\theta}})$`

???
We replace the true `$\boldsymbol \theta$` with an estimator to obtain the EB predictor
nonsampled units `$\bar s_i$`

---
## Conditional Distribution

#### Result 1: 
`$$u_i|\color{red}{b_i}, \boldsymbol{y}^*_{s_i} \sim N(\tilde\mu_{u_i}, \tilde{\sigma}^2_{u_i})$$`
where `$$\tilde\mu_{u_i} = \gamma_i\bar{\tilde{r}}_i+(1-\gamma_i)\Big[\rho\frac{\sigma_u}{\sigma_b}{b_i}\Big], \tilde\sigma_{u_i}^2 = \gamma_i{\sigma_e^2}/{\tilde{n}_i}$$`
and `$\color{blue}{\gamma_i = (1-\rho^2)\sigma_u^2 [(1-\rho^2)\sigma_u^2+\sigma_e^2/\tilde{n}_i]^{-1}}, \tilde{n}_i=\sum_{j\in s_i}\delta_{ij}$`, `$$\bar{\tilde{r}}_i= \tilde{n}_i^{-1}\sum_{j\in s_i} \delta_{ij}\{\log(y_{ij})-\beta_0-\boldsymbol{z}_{1,ij}'\boldsymbol\beta_1\}$$`

**Remark**: when `$\rho=0$`, `$\gamma_i = {\sigma_u^2}/({\sigma_u^2+\sigma_e^2/\tilde{n}_i})$`, `$u_i|\boldsymbol{y}^*_{s_i}\sim N(\gamma_i\bar{\tilde{r}}_i, \gamma_i{\sigma_e^2}/{\tilde{n}_i})$`.

---
## Conditional Distribution (Cont'd)

#### Result 2: 
`$$f(b_i|\boldsymbol{y}_{s_i}^*) \propto \pi_{s_i}(b_i)\phi(\frac{b_i-m_i}{\sqrt{v_i}})$$`
where `$\phi(\cdot)$` is the probability density function of standard normal distribution,
`$$\pi_{s_i}(b_i)=\prod_{j \in s_i}\Big [ p_{ij}\delta_{ij}+(1-p_{ij})(1-\delta_{ij})\Big ]$$`
and `$p_{ij}(b_i)=g^{-1}(\alpha_0+\boldsymbol\alpha_1\mathbf z_{ij}+b_i)$`.
`$$\color{blue}{(m_i, v_{i}) =(\frac{\rho\sigma_u\sigma_b}{\sigma_u^2+\sigma_e^2/\tilde{n}_i}\bar{\tilde{r}}_i,   \frac{1-\rho^2}{1-(1-\gamma_i)\rho^2}\sigma_b^2)}.$$`
**Remark**: when `$\rho=0$`, `$(m_i, v_{i})=(0, \sigma_b^2)$`.

---
## Conditional Distribution (Cont'd)
#### Result 3: 
`$$E(y_{ij}^*|\boldsymbol{y}_{s_i}^*, \boldsymbol\theta) = h_{ij}(\boldsymbol\theta)E(p_{ij}(b_i)\color{blue}{\eta(b_i)}|\boldsymbol{y}_{s_i}^*)$$`
where `$h_{ij}(\boldsymbol\theta) = \exp(\beta_0+x_{ij}'\beta_1+{\gamma_i}\bar{\tilde{r}}_i + \tilde{\sigma}_{u_i}^2/2+\sigma_e^2/2)$` and `$\eta(b_i)=\exp((1-\gamma_i){\rho}\sigma_u/\sigma_b b_i).$`

👉 `$\hat{y}_{ij}^{*\rm{EB}} = E(y_{ij}^*|\boldsymbol{y}_{s_i}^*, \hat{\boldsymbol\theta})$`

**Remark**: The proposed predictor can accommodate any parametrized link (transformation) function for the positive part and the binary part.
---
## Parameter Estimation

Given `$\rho \neq 0$`, how to get a consistent estimator for model parameter `$\boldsymbol\theta = (\boldsymbol\beta', \boldsymbol\alpha', \sigma^2_u, \sigma^2_b, \sigma^2_e, \rho)'$`? 😣

Full likelihood function:
`$$\begin{eqnarray}L_i(\boldsymbol\theta) &=& \frac{(1-\gamma_i)^{1/2}(v_i/\sigma_b^2)^{1/2}}{(2\pi\sigma_e^2)^{\tilde{n}_i/2}}\exp(\frac{\gamma_i\bar{\tilde{r}}_i^2}{2\sigma_e^2/\tilde{n}_i} + \frac{m_i^2}{2v_i}-\frac{\sum_j\tilde{r}_{ij}^2}{2\sigma_e^2}) \\ && \int \pi_{s_i}(b_i)\frac{1}{\sqrt{v_i}}\phi(\frac{b_i-m_i}{\sqrt{v_i}})\mathrm{d}b_i\end{eqnarray}$$`
**Remark**:

+ A good starting value and the gradient vector `$\partial L/\partial\boldsymbol\theta$` help `optim` find the optimizer much faster. ✌️
  
  + Profiling out `$\rho$` takes much longer time to find the MLE.

???
first approach also allows inference for simultaneous confidence interval or hypothesis test

---
## MSE Estimator

Formally, the MSE of an EB predictor is
`$$\rm{MSE}(\hat\zeta_{i}^{EB}) = M_{1i}(\boldsymbol\theta) + M_{2i}(\boldsymbol\theta)$$`
where
`$$M_{1i}(\boldsymbol\theta)=E(\hat\zeta_{i}^{\rm{MMSE}}-\zeta_{i})^2 = O(1), \text{ as } D \to \infty$$`
and
`$$M_{2i}(\boldsymbol\theta)=E(\hat\zeta_{i}^{\rm{EB}}-\hat\zeta_{i}^{\rm{MMSE}})^2 = o(1), \text{ as } D \to \infty$$`
Recall that
`$$\hat\zeta_{i}^{\rm{MMSE}} = E[\zeta_{i}|\boldsymbol{y}_{s_i}^*, \boldsymbol{\theta}], \hat\zeta_{i}^{\rm{EB}} = E[\zeta_{i}|\boldsymbol{y}_{s_i}^*, \hat{\boldsymbol{\theta}}]$$`

???
`$M_{2i}(\boldsymbol\theta)$` results from the parameter estimation process.

---
## MSE Estimator (Cont'd)

So the MSE of the optimal predictor is
`$$M_{1i}(\boldsymbol\theta)=E(E[\zeta_{i}|\boldsymbol{y}_{s_i}^*, \boldsymbol\theta] - \zeta_{i})^2=E[V(\zeta_{i}|\boldsymbol{y}_{s_i}^*, \boldsymbol\theta)]$$`
We propose a **One-Step** MSE estimator defined by
`$$V(\zeta_{i}|\boldsymbol{y}_{s_i}^*, \color{red}{\hat{\boldsymbol\theta}}) = \frac{1}{N_i^2}\sum_{j \in \bar{s}_i}\sum_{k \in \bar{s}_i}\Big[E\{y^*_{ij}y^*_{ik}|\boldsymbol{y}_{s_i}^*, \hat{\boldsymbol\theta}\} - E\{y^*_{ij}|\boldsymbol{y}_{s_i}^*, \hat{\boldsymbol\theta}\}E\{y^*_{ik}|\boldsymbol{y}_{s_i}^*, \hat{\boldsymbol\theta}\}\Big]$$`
where
`$$E\{y^*_{ij}y^*_{ik}|\boldsymbol{y}_{s_i}^*\} = h_{ij}h_{ik}\exp(\tilde{\sigma}_{u_i}^2)E[p_{ij}p_{ik}\color{blue}{\eta(2b_i)}|\boldsymbol{y}_{s_i}^*],j \neq k$$`
and `$$E\{y^*_{ij}y^*_{ik}|\boldsymbol{y}_{s_i}^*\} = h_{ij}^2\exp(\tilde{\sigma}_{u_i}^2+\sigma_e^2)E[{p_{ij}}\color{blue}{\eta(2b_i)}|\boldsymbol{y}_{s_i}^*],j = k$$`

---
## Alternate MSE Estimators

- Denote original parameter estimate `$\hat{\boldsymbol{\theta}}$`, bootstrap population `$\boldsymbol Y^{*(b)}$`, bootstrap sample `$\boldsymbol y^{*(b)}$`, parameter estimate `$\hat{\boldsymbol{\theta}}^{(b)}$`

- For `$b = 1,\ldots, B$`, we obtain
`$$\boldsymbol Y^{*(b)} \longrightarrow \bar{y}_{N_{i}}^{*(b)}$$`
`$$\boldsymbol{y}^{*(b)}, \hat{\boldsymbol{\theta}} \longrightarrow \hat{\bar{y}}_{N_i}^{*(b)\rm{MMSE}}$$`
`$$\boldsymbol{y}^{*(b)}, \hat{\boldsymbol{\theta}}^{(b)} \longrightarrow \hat{\bar{y}}_{N_i}^{*(b)\rm{EB}}$$`

1. `$\hat{\mbox{MSE}}_{i}^{\color{blue}{\mbox{Boot}}} = B^{-1}\sum_{b = 1}^{B}(\hat{\bar{y}}_{N_{i}}^{*(b)\mbox{EB}} - \bar{y}_{N_{i}}^{*(b)})^{2}$`

1. `$\hat{\mbox{MSE}}_{i}^{\color{blue}{\mbox{Semi-Boot}}} = \hat{M}_{1i} + \hat{M}_{2i}^{\mbox{Boot}}$`
where a bootstrap estimator of `$M_{2i}$` is defined by
`$\hat{M}_{2i}^{\mbox{Boot}} = B^{-1}\sum_{b = 1}^{B}(  \hat{\bar{y}}_{N_{i}}^{*(b)\mbox{EB}}  - \hat{\bar{y}}_{N_{i}}^{*(b)\mbox{MMSE}})^{2}$`

---
## Simulation Setting

- Number of areas: `$D = 60$`

- Sample rate: `$(N_i, n_i) = (71, 5), (143, 10), (286, 20)$` for every 20 areas so that `$(N, n)=(10000, 700)$`

- `logit` link for the binary part

- One-dimensional covariates: `$z_{ij}\sim N(4.45, 0.055)$`

- `$\boldsymbol\beta = (-13, 2)', \boldsymbol\alpha = (-20, 5)'$`, `$(\sigma_u^2, \sigma_e^2, \sigma_b^2) = (0.22, 1.23, 0.52)$`

- `$\rho \in \{-0.9, -0.6, -0.3, 0, 0.3, 0.6, 0.9\}$`

- Compare the proposed EB predictor with the EB(0) predictor `$\hat \zeta_{i}^{\rm{EB}}\mid_{\rho=0}$`

**Remark**: the EB(0) predictor (Lyu 2018) is based on `$\hat{\boldsymbol\theta}_0$` obtained from fitting the two parts separately

---
## Simulation Results

`$$\rm{RDMSE}_i = \frac{\rm{MSE}(\hat\zeta_i^{\rm{EB(0)}}) - \rm{MSE}(\hat\zeta_i^{\rm{EB}})}{\rm{MSE}(\hat\zeta_i^{\rm{EB}})}$$`
 
<center><img src="images/EB_EB0_tb.png" width="600"/></center>
<center>Table 1. Relative difference of MSE of the EB(0) predictor compared with the EB predictor based on 1000 simulations.</center>

---
## Simulation Results

`$$\rm{RBMSE}_i = \frac{\hat{\rm{MSE}}_{i} - \rm{MSE}(\hat\zeta_i)}{\rm{MSE}(\hat\zeta_i)}, \rm{CI}_i = \hat\zeta_i\pm1.96\sqrt{\hat{\rm{MSE}}_{i}}$$`
 
<center><img src="images/MSEs.png" width="800"/></center>
Table 2. Relative bias and coverage rate of nominal 95% confidence intervals when `$\rho = 0.9$` for different MSE estimators based on 1000 simulations and 100 bootstrap samples.

???
Estimating the leading term directly seems to improve the quality of CIs based on "Boot" when B = 100

---
## Application to CEAP data
.left-column[
### Data Description
]

.right-column[
#### Response
**RUSLE2**: sheet and rill erosion from cropland tons/yr

#### Auxilliary information
On a cropland grid at a spatial resolution of 56m

**logR** 💦: log-scale county-level Rainfall factor 👈 NRI
  
**logK** 🗻: log-scale erosion factor 👈 Soil Survey
  
**logS** 📐: log-scale slope gradient factor 👈 Soil Survey
  
**crop_type** 🌱: corn, soybean, sprwht or wtrwht 👈 CDL
]

---
## Application to CEAP data
.left-column[
### Data Description
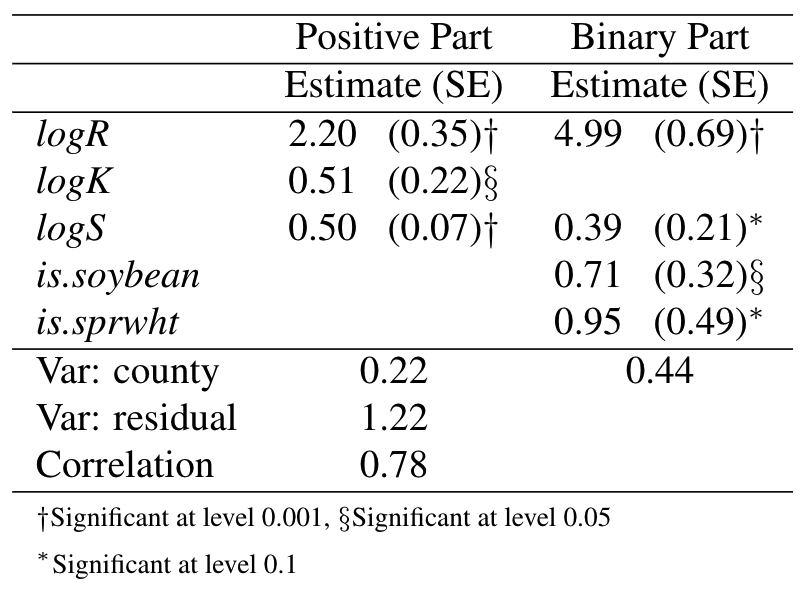
### Parameter Estimates
]

.right-column[
Based on the observed information matrix, 95% confidence interval for `$\rho$` is `$(0.67, 0.84)$`.

<img src="images/para_est.png" width="400"/>
]

---
## Application to CEAP data
.left-column[
### Data Description
### Parameter Estimates
### EB Predictions
]

.right-column[
<img src="images/EB_prediction.png" width="600"/>
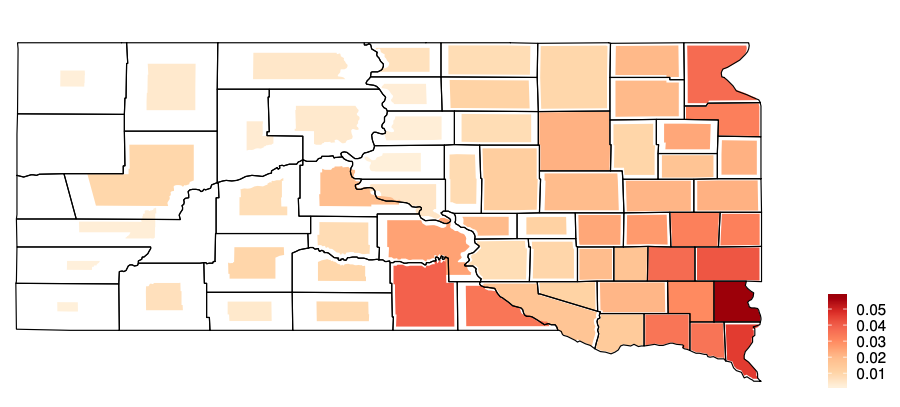Figure 1. Cartogram of the EB predicted county means of cropland RUSLE2 in South Dakota. Smaller shrinkage indicates smaller coefficient of variance.
]

???
Eastern South Dakota: more cropland, more samples, more positive response
Two counties have no sample, many counties have less than 5 samples, some county at most 30 samples.
mean SE around 0.005

---
## Conclusion

- A frequentist approach has been proposed to fit zero-inflated lognormal model with correlated random effects in small area prediction.

- When the true correlation deviates far from 0, the EB(0) predictor (Lyu 2018) has moderately larger MSE than the EB predictor (without model mis-specification).

- The data analysis of the cropland CEAP RUSLE2 measurements collected in South Dakota shows the model assumptions are reasonable.

---
background-image: url(https://media.giphy.com/media/jlcvK6qs6PJtQIoIYW/giphy.gif)
background-position: 50% 50%
background-size: 50%

---
count:false
## Appendix A: CEAP RUSLE2 Residual Analysis

Positive part fitted value: marginal 👉 `$\boldsymbol{x}_{ij}'\hat{\boldsymbol{\beta}}$`, conditional 👉 `$\boldsymbol{x}_{ij}'\hat{\boldsymbol{\beta}} + \hat{E}[u_{i} | \boldsymbol{y}_{s_i}^*]$`
 + marginal residual (top): `$(\mbox{log}(y_{ij}) - \boldsymbol{x}_{ij}'\hat{\boldsymbol{\beta}})/\sqrt{\hat{\sigma}^{2}_{u}+ \hat{\sigma}^{2}_{e}}$`
 + conditional residual (bottom): `$(\mbox{log}(y_{ij}) - \boldsymbol{x}_{ij}'\hat{\boldsymbol{\beta}} - \hat{E}[u_{i} | \boldsymbol{y}_{s_i}^*])/\sqrt{\hat{\sigma}^{2}_{e}}$`

---
count:false
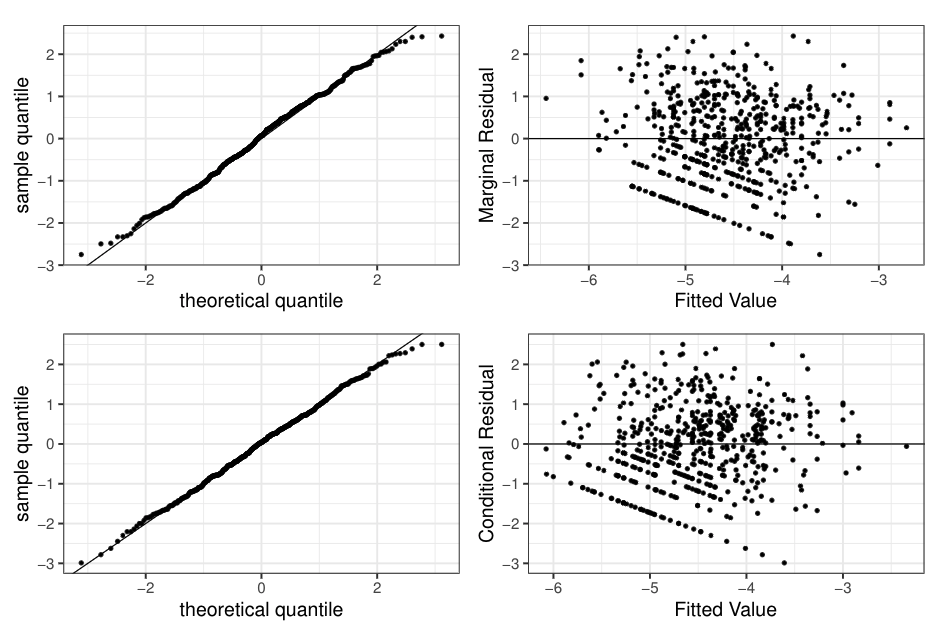
## Appendix A: CEAP RUSLE2 Residual Analysis

Binary part: Hosmer-Lemeshow test with `$\hat{p}_{ij} = E[p_{ij}(b_i) | \boldsymbol{y}_{s_i}^*]$`

---
count:false
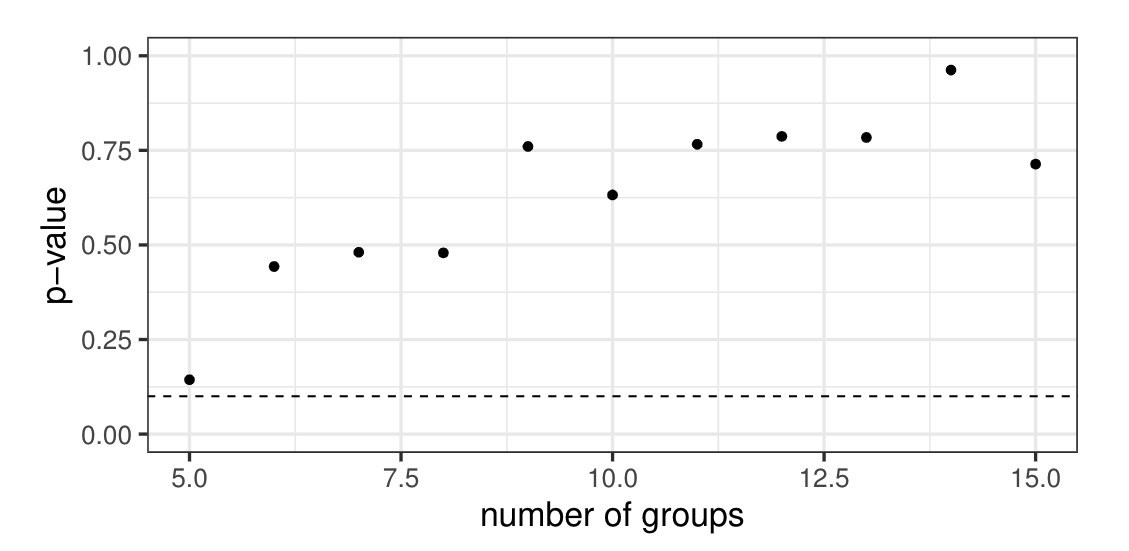
## Appendix B: Simulation results

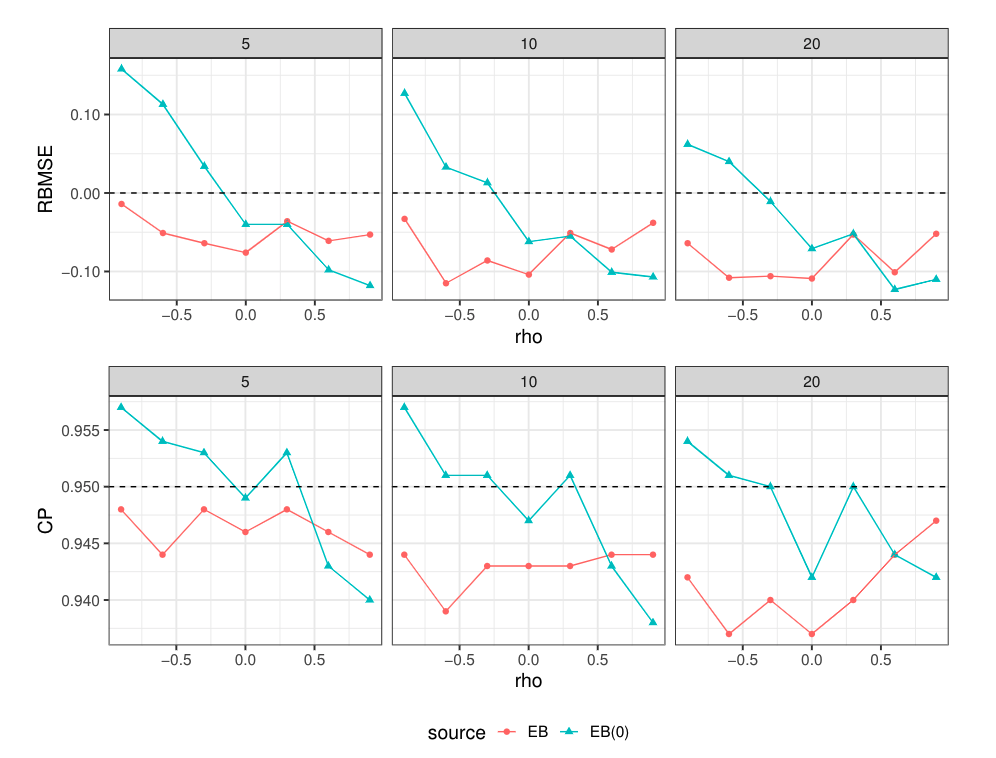
<center><img src="images/EB_EB0.png" width="550"/></center>
<center>Relative bias and coverage rate of nominal 95% confidence intervals for the EB and the EB(0) predictor based on 1000 simulations.</center>